Vamos a continuar hoy elaborando la función de lo que se puede llamar el significante del corte, o aún el 8 interior, o aún el lazo (lac), o aún lo que llamé la última vez el significante polaco. Quisiera poder darle un nombre aún menos significativo para intentar cernir lo que tiene de puramente significante.
Hemos avanzado sobre este terreno tal como se presenta, es decir en una notoria ambigüedad, ya que, pura línea, nada indica que se recorte como la forma en que la he dibujado ahí -ustedes lo recuerdan- pero al mismo tiempo dejo abierta la posibilidad de ese recorte. En suma, este significante no prejuzga nada del espacio donde se sitúa. Sin embargo, para hacer de esto algo, planteamos que es en torno a este significante del corte que se organiza lo que llamamos la superficie en el sentido en que la entendemos aquí.
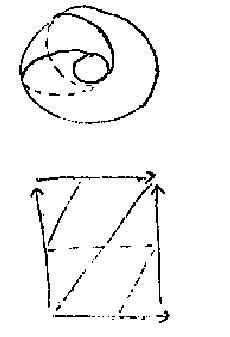
La última vez les recordaba -pues no es la primera vez que lo mostré ente ustedes- cómo puede construirse la superficie del toro en torno, y en torno solamente, de un corte, de un corte ordenado, manipulado de esta manera cuadrilátera que la fórmula expresada por la sucesión de un A, de un B, luego de un A’ y de un B´, respectivamente nuestros testigos en la medida en que pueden ser referidos, pegados a los dos precedentes en una disposición que podemos calificar en general por dos términos: orientada por una parte, atravesada por otra.
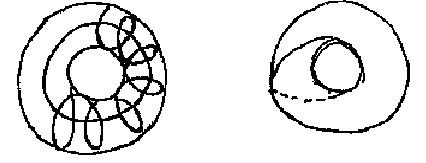
Les he mostrado la relación, la relación si se puede decir ejemplar en un primer aspecto, metafórica cuya cuestión justamente es la de saber si esta metáfora supera, si se puede decir, el puro plano de la metáfora, la relación metafórica, digo, que puede tomar de la relación del sujeto al Otro, a condición de que explorando la estructura del toro percibamos que podemos poner dos toros encadenados uno al otro en un modo de correspondencia tal que a tal círculo privilegiado sobre uno de los dos que hemos hecho corresponder por razones analógicas a la función de la demanda, a saber esta suerte de círculo giratorio (tournant) en la forma familiar de la bobina que nos parece particularmente propicia para simbolizar la repetición de la demanda, en la medida en que acarrea esta suerte de necesidad de anillarse (se boucler), si se excluye que se recorte después de numerosas repeticiones tan multiplicadas como podamos suponerlo ad libitum, por haber hecho este anillado (bouclage), haber dibujado la vuelta, el contorno de otro vacío que aquel que ella cierne, el que hemos distinguido primero, definiéndole este lugar de la nada cuyo circuito dibujado por sí mismo nos sirve para simbolizar bajo la forma del otro circulo topológicamente definido en la estructura del toro, el objeto del deseo.
Para aquellos entonces que no estaban acá voy a ilustrar lo que vengo de decir por esta forma simple, repitiendo que este bucle del ambobinamiento de la demanda que se encuentra en torno al vacío constitutivo del toro-se encuentra dibujado lo que nos sirve para simbolizar zar el circulo del objeto del deseo; a saber todos los círculos que dan la vuelta al agujero central del anillo.
Hay entonces dos clases de círculos privilegiados sobre un toro:
-aquellos que se dibujan en torno del agujero central
-aquellos que lo atraviesan.
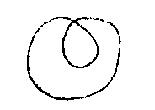
Un círculo puede acumular las dos propiedades. Es precisamente lo que sucede con ese círculo dibujado así:
Lo pongo puntillado cuando pasa del otro lado.
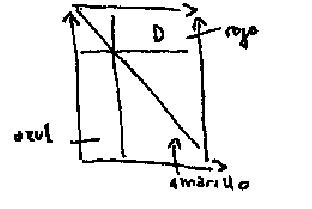
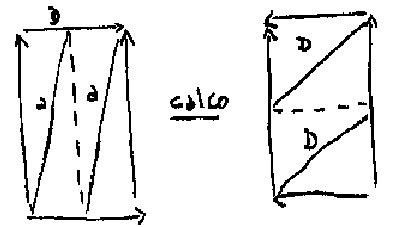
Sobre la superficie cuadrilátera del polígono fundamental que sirve para mostrar de una manera clara y unívoca la estructura del toro, simbolizo aquí para emplear los mismos colores, de aquí hasta aquí un circulo llamado círculo de la demanda, de ahí hasta acá, un círculo llamado círculo a, simbolizando el objeto del deseo. Y es ese círculo que ustedes ven sobre la primer figura, que está aquí dibujado en amarillo, representando el círculo oblicuo, que podría en rigor servirnos para simbolizar como corte del sujeto al deseo mismo.
El valor expresivo, simbólico, del toro, es precisamente el de hacernos ver la dificultad, en la medida en que se trata de la superficie del toro y no de otra, de ordenar ese círculo, aquí amarillo del deseo, con el circulo, aquí azul, del objeto del deseo.
Su relación es tanto menos unívoca cuanto que el objeto no es aquí fijo, determinado por ninguna otra cosa que por el lugar de una nada que, si se puede decir, prefigura su lugar eventual,. pero de ninguna manera permite situarlo. Tal el valor ejemplar del toro.
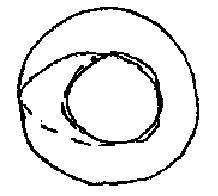
Ustedes han entendido la última vez que este valor ejemplar se completa con esto de que al suponerlo encadenado, concatenado con otro toro que simbolizarla al Otro, vemos que seguramente esto -se los he dicho- se demuestra -les he dejado la tarea de encontrar ustedes mismos esta demostración, para no retrasarnos-, vemos que seguramente al calcar así el circulo del deseo proyectado sobre el primer toro –sobre el toro que se encaja (emboite) a él simbolizando el lugar del Otro -encontramos un círculo orientado de la misma manera.
Recuerden, ustedes tienen representado frente a esta figura que retomaré si la cosa no les parece demasiado fastidiosa, el calco que es una imagen simétrica. Tenemos entonces una línea oblicua, orientada de sur a norte que podemos decir invertida, especular hablando con propiedad. Pero la báscula de 90 grados que corresponde al encaje (emboitement) a 90° de los dos toros restituirá la misma oblicuidad. Dicho de otro modo, después de haber tomado efectivamente -son experiencias muy fáciles de realizar, que tienen todo el valor de una experiencia esos dos toros y haber hecho efectivamente por el método de rotación de un toro en el interior del otro que les he designado la última vez ese calco, habiendo relevado, si se puede decir, la traza de esos dos círculos arbitrariamente dibujados sobre uno y determinado desde entonces sobre el otro, podrán ver al compararlos a continuación que son exactamente, en el círculo que los seccióna, superponibles uno al otro.
¿En qué se revela entonces esta imagen apropiada para representar la fórmula de que el deseo del sujeto es el deseo del Otro?.
Sin embargo, les he dicho, si suponemos no ese simple círculo dibujado en esta propiedad, en esta definición topológica particular de rodear a la vez y atravesar el agujero, sino de hacerle dos veces atravesar el agujero, y de una sola vez su entorno, es decir sobre el polígono no fundamental de presentarse así (croquis),. siendo esos dos puntos aquí equivalentes, tenemos entonces algo que sobre el calco, a nivel del Otro. se presenta según la fórmula siguiente:
Si ustedes quieren, digamos, que la realización de dos veces la vuelta, que corresponde a la función del objeto y a la transferencia sobre el calco sobre el otro toro, en dos veces, de la demanda según la fórmula de equivalencia que es para nosotros preciosa en esta ocasión, es simbolizar el hecho de que en una cierta forma de estructura subjetiva, la demanda del sujeto consiste en el objeto del Otro, el objeto del sujeto consiste en la demanda del Otro.
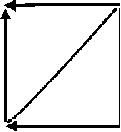
Recorte: entonces la superposición de dos términos, después de la báscula, no es más posible.
Después de la báscula de 90° (croquis) el corte es éste, el cual no se superpone a la forma precedente.
Hemos reconocido ahí la correspondencia que nos es familiar desde siempre, en la medida en que lo que podemos expresar de la relación del neurótico al Otro en tanto condiciona en último término su estructura es precisamente esta equivalencia cruzada (croisée) de la demanda del sujeto al objeto del Otro, del objeto del sujeto a la demanda del Otro. Se percibe ahí en una suerte de impasse o al menos de ambigüedad la realización de la identidad de dos deseos.
Esto está evidentemente tan abreviado como es posible como fórmula y supone seguramente una familiaridad ya adquirida con esas referencias las que suponen todo nuestro discurso anterior.
La cuestión entonces queda abierta, siendo aquella que vamos a dar hoy de una estructura que nos permite formalizar de una manera ejemplar, rica en recursos, en sugestiones, que nos da un soporte que es hacia el cual se encamina precisamente nuestra búsqueda, a saber la función del fantasma, es a este fin que puede servirnos la estructura particular llamada cross-cap o plano proyectivo, en la medida en que también ya les he dado una indicación suficiente sobre él como para que este objeto les sea si no absolutamente familiar al menos que ya los haya tentado de profundizar lo que presenta como propiedades ejemplares.
Me excuso entonces de entrar, a partir de ahora, en una explicación que, por el momento, va a quedar estrechamente ligada a este objeto de una geometría particular llamada topológica , geometría no métrica sino topológica, de la que les he hecho observar tanto como he podido al pasar la idea que debe hacerse de ella, presto a lo cual, luego de haber hecho el esfuerzo de seguirme, en lo que sigue, en lo que voy ahora a explicarles serán recompensados por lo que nos permitirá soportar como fórmula que concierne a la organización subjetiva, que es la que nos interesa, por lo que nos permitirá ejemplificar la estructura auténtica del deseo en lo que se podría llamar su función central organizadora.
No dejo de tener, por supuesto, cierta reluctancia en el momento, una vez más, de llevarlos sobre terrenos que pueden fatigarlos. Es porque me referiré un momento a dos términos que se encuentran próximos en mi experiencia y que van a darme la oportunidad -de entrada primera referencia- de anunciarles la aparición eminente de la traducción hecha por alguien eminente que nos hace hoy el honor de su visita, a saber M. de Wahlens, que viene de hacer la traducción -de la que uno no estarla nunca demasiado sorprendido de que no haya sido realizada antes de «Ser y Tiempo», «Sein und Zeit», al menos de llevar hasta su punto de acabamiento la primer parte del volúmen aparecido del que ustedes saben no es sino la primer parte de un proyecto cuya segunda parte no ha aparecido nunca. Entonces en esta primera parte hay dos secciónes, y la primera sección es ahora traducida por M. de Wahlens que me ha hecho el gran honor, el favor, de comunicármelo lo que me ha permitido tomar conocimiento yo mismo de esta parte -la mitad aún solamente- y debo decir con infinito placer, un placer que va a permitirme un segundo el de decir finalmente, a este respecto, lo que tengo en el corazón desde hace mucho y me he dispensado siempre de profesar en público, porque en verdad, vista la reputación de esta obra de la que no creo muchos de acá la hayan leído habría tenido la apariencia de una provocación.
Es esto: es que hay pocos textos más claros, finalmente de una claridad y una simplicidad concreta y en fin directa -no sé cuales son las calificaciones que es necesario invente para agregar una dimensión suplementaria a la evidencia que los textos de Heidegger. No es porque lo que haya hecho de él Sartre sea efectivamente bastante difícil de leer que esto quite nada al hecho de que este texto -de Heidegger- no digo: todos los otros -es un texto que lleva en sí mismo esta Suerte de superabundancia de claridad que lo vuelve verdaderamente accesible sin ninguna dificultad a toda inteligencia no intoxicada por una enseñanza filosófica previa.
Puedo decirlo ahora porque ustedes tendrán pronto la ocasión de percibirlo gracias a la traducción de M. de Wahlens: verán hasta qué punto es así.
La segunda observación es ésta: que ustedes podrán constatar al mismo tiempo: son vehiculizadas aserciones en folículos extraños por una habladora de profesión de que mi enseñanza es neo-heideggeriana. Esto fue dicho con una intención nociva. La persona probablemente ha puesto neo en razón de una cierta prudencia; como no sabía ni lo que quería decir heideggeriana ni tampoco lo que quería decir mi enseñanza, eso la ponla a cubierto de un cierto número de refutaciones de que esta enseñanza que es la mía no tiene verdaderamente nada de neo, ni de heideggeriana, a pesar de la excesiva reverencia que tengo por la enseñanza de Heidegger.
La tercera observación está ligada a una segunda referencia, a saber que algo va a aparecer -ustedes serán obsequiados pronto- que es al menos tan importante -finalmente la importancia no se mide en dominios diferentes con un centímetro- que es muy importante también: es el volumen -que no esta aún en librerías, según me han dicho- de Claude Lévy-Strauss que se llama «El pensamiento salvaje».
Ha aparecido me dice usted. Espero que ya haya comenzado a divertirse gracias a las preocupaciones que me impone nuestro seminario, no he avanzado muy lejos, pero he leído las páginas inaugurales magistrales por donde Claude Lévy-Strauss entra en la interpretación de lo que se llama Le Pensamiento salvaje, que hay que entender como en su entrevista en el Figaro, pienso, se los ha ya enseñado- no como el pensamiento de los salvajes, sino como lo que se puede decir el estado salvaje del pensamiento, digamos el pensamiento en tanto que funciona bien, eficazmente, con todos los carácteres del pensamiento, antes de toda forma de pensamiento científico, del pensamiento científico moderno con su estatuto. Y Claude Lévy-Strauss nos muestra que es absolutamente imposible poner ahí un corte tan radical en tanto el pensamiento que todavía no ha conquistado su estatuto científico es ya absolutamente apropiado para portar algunos efectos científicos.
Tal es por lo menos su propósito aparente en la partida, y toma singularmente como ejemplo para ilustrar lo que quiere decir del pensamiento salvaje algo donde sin duda entiende reunir eso de común que tendría con el pensamiento, digamos tal que, él lo subraya, tal como ha dado frutos fundamentales a partir del momento mismo que no se puede calificar absolutamente de ahístórico en tanto lo precisa: el pensamiento a partir de la era neolítica que da, nos dice, aún todos sus fundamentos a nuestro asiento en el mundo. Para ilustrarlo, si puedo de oír, aún funcionando a nuestro alcance, no encuentro otra cosa ni nada mejor que ejemplificarlo bajo una forma sin duda no única pero privilegiada por su demostración bajo la forma que se llama el bricolaje.
Este pasaje tiene todo el brillo que le conocemos, la originalidad propia de esta suerte de abrupto, de novedad, de cosa que báscula y reinvierte las perspectivas banalmente recibidas, y es un fragmento seguramente fuertemente sugestivo.
Otro me ha parecido particularmente sugestivo luego de la relectura que acababa de hacer de Heidegger gracias a M. de Wahlens, precisamente en tanto él toma como ejemplo de su búsqueda del estatuto, si se puede decir, del conocimiento, en tanto que puede establecerse de una aproximación (aproche) que para establecerlo pretende encaminar a partir de la interrogación concerniente a lo que se llama el ser-ahí , es decir la forma más velada a la vez y la más inmediata de un cierto tipo de ente (étant), el hecho de ser que es aquél particular al ser humano, uno no puede dejar de ser sorprendido, aún cuando probablemente la observación indignarla tanto a uno como a otro de estos autores, de la sorprendente identidad sobre la cual uno y otro avanzan.
Quiero decir que lo encuentra de entrada Heidegger en esta búsqueda, una cierta relación del ser ahí a un ente (étant) que es definido como utensilio, herramienta, como útil, como algo que se tiene en la mano del que se sirve, como Zuhandenheit para lo que esta en la mano.
Tal es la primer forma de lazo, no al mundo sino al ente (étant) que Heidegger nos designa. Y es solamente a partir de ahí, a saber, si se puede decir, en las implicaciones, la posibilidad de semejante relación, que él va, dice, a dar su estatuto propio a lo que constituye el primer gran pivote de su análisis la función del ser en su relación con el tiempo, a saber la Welltlicheit que M. de Wahlens ha traducido por las «mundanidades», a saber la constitución del mundo de alguna manera previa, previa a ese nivel del ser-ahí que no se ha destacado aún en el interior del ente (étant), esas suertes de ente que podemos considerar como pura y simplemente subsistiendo por sí mismos.
El mundo es otra cosa que el conjunto, el englobamiento de todos esos seres que existen, subsisten por sí mismos, con los cuales tenemos que vérnoslas a nivel de esta concepción del mundo que nos parece tan inmediatamente natural -y con motivo- porque es aquélla que llamamos naturaleza. la anterioridad la constitución de esta modernidad en relación al momento en que podemos considerarla como naturaleza, tal es el intervalo que preserva, por su análisis, Heidegger.
Esta relación primitiva de instrumentalidad (ustensilité) prefigurando el Umwelt anterior aún al entorno que no se constituye, por relación a él sino secundariamente, está ahí la búsqueda de Heidegger, y es exactamente la misma -no creo decir nada por ahí que pueda ser retenido como critica que ciertamente después de todo lo que conozco del pensamiento y los decires de Levy-Strauss, nos parecería la búsqueda más opuesta a la suya en la medida en que lo que él da como estauto a la investigación etnográfica no se produciría sino en una posición de aversión en relación a la búsqueda metafísica o incluso ultrametafísica de Heidegger. por tanto, es la misma que encontramos en ese primer paso por el cual Claude Lévy-Strauss cree introducirnos al pensamiento salvaje bajo la forma de ese bricolage que no es otra cosa que el mismo análisis, simplemente te en términos diferentes, un esclarecimiento apenas modificado. Una mira sin duda distinta de esa misma relación a la instrumentalidad (ustensilité) como siendo lo que uno y otro consideran como anterior, como primordial en relación a esta suerte de acceso de estructura, de acceso estructurado que es el nuestro en relación al campo de la investigación científica, en tanto permite distinguirlo como fundado sobre una articulación de la «objetividad» que es de alguna manera autónoma, independiente de lo que es propiamente hablando nuestra existencia, y que no conservamos con él más que esa relación llamada «sujeto-objeto» que es ese punto donde se resume todo lo que podemos articular de la epistemología hoy día.
Y bien , digamos para fijarlo de una vez, lo que nuestra empresa aquí en tanto que fundada sobre la experiencia analítica tiene de distinto en relación a una y a la otra de esas investigaciones cuya carácter paralelo vengo de mostrarles. Es que nosotros también aquí buscamos el estatuto, si se puede decir, anterior al acceso clásico del estatuto del objeto, enteramente concentrado en la oposición sujeto-objeto ¿Y lo buscamos en qué? En algo que, sea cual fuere el carácter evidente de aproximación, de atracción en el pensamiento, tanto de Heidegger como en Levy-Strauss, éste es distinto, pues ni uno ni otro nombra como tal a este objeto como objeto de deseo.
El estatuto primordial del objeto para digamos en todo caso un pensamiento analítico no puede ser y no podría ser otro que el objeto del deseo. Todas las confusiones con que se tropieza hasta aquí en la teoría analítica son consecuencia de esto: de una tentativa, de más de una tentativa, de todos los modos posibles de tentativa por reducir lo que se nos impone, a saber esta búsqueda del estatuto del objeto del deseo, para reducirlo a referencias ya conocidas de las que la más simple y común es la del objeto de la ciencia en tanto que una epistemología filosofante la organiza en la oposición última y radical sujeto-objeto en tanto que una interpretación más o menos influenciada por los matices de la búsqueda fenomenológica puede en rigor hablar como del objeto del deseo.
Ese estatuto del objeto del deseo como tal queda siempre eludido en todas sus formas hasta aquí articuladas de la teoría analítica; y lo que buscamos aquí es precisamente darle su estatuto propio. Es en esta línea que se sitúa la mira que pondré ante ustedes, por el momento.
Tenemos en las figuras en que hoy voy a intentar hacerles observar lo que nos interesa en esta estructura de superficie cuyas propiedades privilegiadas están hechas para retenernos como soporte estructurante de esa relación del sujeto al objeto del deseo, en tanto que se sitúa como soportando todo lo que podemos articular al nivel que sea en la experiencia analítica, dicho de otro modo como ente estructura que llamamos del fantasma fundamental.
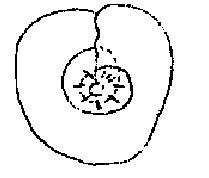
Para aquellos que no estuvieron en el seminario precedente, recuerdo esta forma aquí (croquis) dibujado en blanco: es la que llamamos cross-cap o para ser precisos -pues se los he dicho, una cierta ambigüedad queda sobre el uso de ese término cross-cap: el plano proyectivo.
Como su dibujo aquí en tiza basta, para aquellos que no lo han aprehendido aún, para hacerles representar lo que es, voy a intentar hacérselos imaginar describiéndoselos como si esta superficie estuviera ahí constituida en goma.
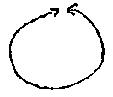
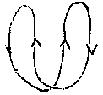
Para ser aún más claro, voy a partir de la base. Supongan que tienen dos arcos como los de una trampa para lobos (croquis). Esto va a servirnos para representar el corte. Si orientamos los dos círculos de la trampa para lobos en el mismo sentido, esto quiere decir que vamos simplemente a cerrarlos uno sobre el otro. Si tienen una película, precisamente si ustedes soplan dentro y si cierran la trampa para lobos, está enteramente al alcance de las imaginaciones más elementales, ven que van a hacer una esfera.
Si el soplo no les parece suficiente llenen de agua hasta que obtengan esta forma, cierren los dos semi-círculos de la trampa para lobos, y tienen una esfera semiplena o semi-vacía.
Les he ya explicado cómo en lugar de esto se puede hacer un toro. Un toro es esto: ponen las dos puntas de ese pañuelo juntas en el aire así y los dos otros por debajo así, y esto basta para hacer, un toro. Lo esencial del toro está ahí, pues: ustedes tienen ahí el agujero central y aquí el vacío circular en torno al cual gira el circuito de la demanda. Es esto lo que el polígono fundamental del toro les ha ya ilustrado. Un toro no es del todo como una esfera. Naturalmente un cross-cap no es en absoluto una esfera tampoco.
El cross-cap, lo tienen aquí (croquis). Deben imaginarlo por esta mitad inferior, realizado como la mitad de lo que han hecho hace un rato con la película (baudruche) cuando la llenaron de aire o de agua; en la parte superior, lo que es aquí anterior vendrá a atravesar lo que es contínuo, lo que es aquí posterior. Las dos caras se cruzan una a la otra, dan la apariencia de penetrarse; en tanto las convenciones concernientes a las superficies son libres- pues no olviden que no las consideramos más, que como superficies, que podemos decir que
sin duda las propiedades del espacio tal como las imaginamos nos fuerzan, en la representación, a representarlas como penetrándose pero basta que no tengamos en absoluto en cuenta esta línea de intersección en ninguno de los momentos de nuestro tratamiento de esta superficie para que todo ocurra como si la tomáramos por nada. No es sino algo que estamos obligados a representarnos porque queremos representar aquí esta superficie, como una línea de penetración, Pero esta línea, si se puede decir, en la constitución de la superficie no tiene ningún privilegio. Me dirán: ¿qué significa lo que está por decir?
X en la sala: —¿acaso esto quiere decir que usted admite, con la estética trascendental de Kant, la constitución fundamental del espacio en 3 dimensiones, en tanto nos dice que–para representar así las cosas usted está obligado a pasar por algo que en la representación es de alguna manera incómodo?
Seguramentede una cierta manera si. Todos aquellos que articulan lo que concierne a la topología de las superficies como tal parten, es el abc de la cuestión, de esta distinción de lo que se puede llamar las propiedades intrínsecas de la superficie y las propiedades extrínsecas. Nos dirán que todo lo que van a articular, determinar, concerniente al funcionamiento de las superficies así definidas, debe distinguirse de lo que ocurre -como se expresan literalmente, cuando se sumerge dicha superficie en el espacio, particularmente en el caso presente, de tres dimensiones.
Es esta distinción fundamental, que es también la que les he sin cesar recordado para decirles que no debemos considerar el anillo, el toro como un sólido y que, cuando hablo del vacío central, del contorno del anillo, como del agujero que es, si se puede decir, axial, son términos que conviene tomar en el interior de esto que no tenemos que hacerlos funcionar en la medida en que apunta» e pura y simplemente a la superficie.
No queda menos que es en la idea de que, como se expresan los topólogos, nos sumergimos en un espacio que podemos dejar en el estado de x -en cuanto al número de dimensiones que lo estructuran, no estamos forzados a prejuzgar- que podemos poner en valor tal o cual de las propiedades intrínsecas de las que se trata en una superficie.
Y la prueba es justamente ésta: es que no tendremos ninguna dificultad en representarnos el toro en el espacio de tres dimensiones que nos es intuitivamente familiar en tanto que para éste tendremos sin embargo una cierta dificultad pues nos será necesario agregar la pequeña nota de toda suerte de reservas concernientes a lo que tenemos que leer cuando intentamos representar en este espacio esta superficie.
Es lo que nos permitiré plantear justamente la cuestión de la estructura de un espacio en tanto que él admite o no admite superficies tales como las que hemos constituido anteriormente.
Hechas estas reservas, les ruego ahora proseguir y considerar lo que les he de enseñar sobre esta superficie precisamente en tanto que es a propósito de su representación en el espacio que voy a intentar poner en valor algunos de sus carácteres que no son por esto menos intrínsecos.
Pues si de aquí en más he eliminado el valor que podemos dar a esta línea de penetración cuyo detalle ven aquí ilustrado es así como podemos representarlas (ver croquis)-que no hay nada sino la manera con que la he dibujado en el pizarrón, que nos plantea un problema.
¿El valor de este punto es un valor que podamos de alguna manera borrar como el valor de esta línea? ¿Acaso este punto es también algo que no se debe sino a la necesidad de la representación en el espacio de tres dimensiones? Se los diré enseguida para esclarecer un poco por adelantado mi propósito: ese punto en cuanto a su función no es eliminable, al menos en un cierto nivel de la especulación sobre la superficie, un nivel que no esta sólo definido por la existencia del espacio de tres dimensiones.
En efecto, ¿qué significa radicalmente la construcción de esta superticie llamada cross-cap, en tanto se organiza a partir del corte que les he hecho representado como una trampa para lobos que se cierra?
Nada más simple que ver que es necesario que esa trampa para lobos sea bipartita, cuando se trata de la esfera, pues es necesario que se repliegue en alguna parte, que sus dos mitades estén orientadas en el mismo sentido: el terminus a quo se distinguirá entonces del terminus ad quus en tanto que deben recubrirse por su longitud.
Podemos decir que aquí (croquis) tenemos la manera con que funciona una en relación a la otra las dos mitades del borde que se trata de reunir para constituir un plano proyectivos.
Aquí (croquis) están orientadas en sentido contrario, lo que quiere decir que un punto situado en este lugar, punto a por ejemplo, corresponderá, será idéntico, equivalente a un punto situado en este lugar en a’ diametralmente opuesto, que otro punto b situado aquí por ejemplo se remitirá a otro punto b’ situado diametralmente.
No nos incita esto a pensar que dada esta relación antipódica de los puntos sobre ese circuito orientado de una manera continua siempre en el mismo sentido, ningún punto tendrá privilegio y que, sea cual fuere nuestra dificultad de intuir de lo que se trata, tenemos simplemente que pensar esa relación circular antipódica como una suerte de entrecruzamiento radiado (rayonné) si se puede decir, que concentra el intercambio de un punto al punto opuesto del borde único de ese agujero, y que lo concentra, si se puede decir, en torno a un vasto entrecruzamiento central que escapa a nuestro pensamiento y que no nos permite de ninguna manera entonces dar una representación satisfactoria de esto.
Sin embargo lo que justifica que las cosas estén así representadas es que hay algo que conviene no olvidar: es que no se trata de figuras métricas, a saber que no es la distancia de a a A, y de a’ a A la que regla la correspondencia punto por punto que nos permite construir la superficie organizando de esta manera el corte, sino únicamente la posición relativa de los puntos, dicho de otra manera en un conjunto de tres puntos que se sitúa sobre la mitad – admitan el uso del termino mitad del que me sirvo en esta ocasión, que está ya representado por la referencia analógica que he hecho aquí de dos mitades del borde- es en tanto sobre ese borde, sobre esta línea, como sobre toda línea, un punto puede ser definido como estando entre otros dos, que un punto c por ejemplo va a poder encontrar su correspondiente en el punto c’ del otro lado… Pero si no tenemos punto de origen, de punto Ultimo señalamiento: en nuestros apuntes, al comienzo de uno de nuestros años científicos, alguien intentó articular de una cierta manera la función transferencial más radical ocupada por el analista en tanto tal. Es ciertamente una aproximación que no es en absoluto de descuidar que haya llegado a articular crudamente, y a mi fe, que pueda tener el sentimiento de que es algo de caradurismo que el analista en función tenga el lugar del falo; ¿qué es lo que esto puede querer decir?
Que el falo al Otro es muy precisamente lo que encarna, no al (escritura en giego), aunque su satisfacción sea aquella del factor por el cual el objeto que sea es introducido a la función de objeto de deseo, sino aquella del deseante, del (escritura en giego).
San Juan VIII-25 como se dice en el Evangelio lo que ha prestado a tales dificultades de traducción que un pensador de Franche-Conté ha creído deber decirme: «Es ahí que se le reconoce: el único pasaje del Evangelio sobre el cual nadie puede acordar es el que usted ha puesto en el epígrafe para una parte de vuestro Informe de Roma» (escritura en griego) el comienzo, si no hay esos puntos de comienzo en alguna parte, es imposible definir un punto como estando entre otros dos, pues c y c’ están también entre esos dos otros a y B si no hay A A’ para ubicar de una manera unívoca lo que ocurre en cada segmento.
Es entonces por otras razones que la posibilidad de representarlos en el espacio que tenemos que definir un punto de origen en este intercambio entrecruzado que constituye la superficie del plano proyectivo entre un borde que es necesario, a pesar de que giro siempre en el mismo sentido, que dividamos en dos.
Esto puede parecerles muy fastidioso, pero verán que va a tomar un interés cada vez mayor.
Les anuncio enseguida lo que quiero decir.
Quiero decir que ese punto (escritura en griego) origen, tiene una estructura absolutamente privilegiada, que es él, su presencia, la que asegura el bucle interior de nuestro significante polaco, un estatuto que le es absolutamente especial.
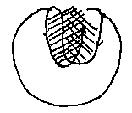
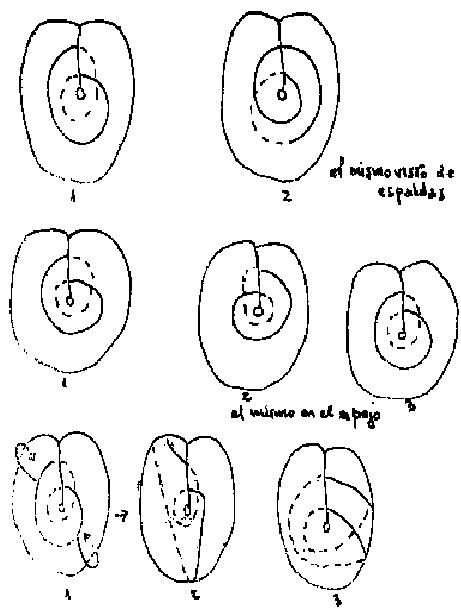
En efecto, para no hacerlos esperar mucho tiempo, aplico este significante, llamado ocho interior, sobre la superficie del cross-cap. Veremos luego qué quiere decir que esta línea que dibuja nuestro significante ocho interior se encuentra aquí dando dos veces la vuelta a ese punto privilegiado (croquis).
Ahí, hagan un esfuerzo de imaginación. Quiero ilustrárselos por algo; vean lo que esto puede dar (croquis).
Tienen ahí, si quieren, el inflamiento de la mitad inferior, el inflamiento de la pinza izquierda de la pata de langosta, el inflamiento (hinchazón) de la pinza derecha.
Ahí ésta entra en el otro, pasa del otro lado. ¿Que quiere decir? Que ustedes tienen en suma un plano que se enrula como éste sobre él, luego que en un momento se atraviesa a sí mismo. De suerte que esto hace como dos especies de postigos o de alas batientes aquí superpuestas que se encuentran en suma aisladas por el corte del inflamiento (hinchazón) inferior, y a nivel superior esas dos alas se cruzan la una a la otra. No es demasiado inconcebible.
Si se interesan tanto tiempo como yo en este objeto, evidentemente les parecerá poco sorprendente. Pues en verdad el privilegio de este doble corte es muy interesante es muy interesante en el sentido que en lo concerniente al toro, se los he mostrado, si hacen un corte transforma en una banda; si hacen un segundo que atraviese el primero- éste no lo fragmenta sin embargo, es lo que les permite extenderlo como un lindo cuadrado. Si hacen hacen cortes que no efe se crucen, sobre un toro -intenten imaginarlo- ahí forzosamente lo ponen en dos pedazos.
Aquí sobre el cross-cap, con un corte que es un corte simple, como el que puede dibujarse así (croquis) ustedes abren esta superficie. Diviértanse haciendo el dibujo, será un buen ejercicio intelectual saber lo que ocurre en ese momento. Ustedes abren la superficie, no la cortan en dos, no hacen dos pedazos.
Si hacen cualquier otro corte que se cruce o que no se cruce la dividen.
Lo que es paradojal e interesante es en suma que no se trata aquí de un sólo corte siempre y que sin embargo, simplemente haciéndole dar dos veces la vuelta del punto privilegiado, dividen la superficie.
No es en absoluto lo mismo en el toro. Sobre un toro, si dan tantas veces como quieran la vuelta del agujero central no obtendrán nunca sino el alargamiento de alguna manera de la banda, pero sin embargo no la dividirán. Esto para hacerles notar que tocamos aquí, sin duda, algo interesante en lo concerniente a la función de esta superficie. Hay por otra parte algo que no es menos interesante: es que esa doble vuelta con su resultado, es algo que no pueden repetir una sola vez si dan una triple vuelta, serán llevados a dibujar sobre la superficie algo que se repetirá indefinidamente a la manera de bucles que ustedes operan sobre el toro, cuando se entregan a la operación de bobinaje de la que les hablé al principio, con la salvedad de que aquí la línea no se reunirá jamás, no se morderá jamás la cola.
El valor privilegiado de esa doble vuelta está entonces suficiente mente asegurado por esas dos propiedades.
Consideremos ahora la superficie que aísla esa doble vuelta sobre un plano proyectivo. Les haré observar algunas propiedades.
De entrada es lo que podemos llamar una superficie -llamémosla como ésta, por la rapidez, entre nosotros, si se puede decir, -es una superficie izquierda, como un cuerpo izquierdo, como cualquier cosa que podamos definir así en el espacio. No lo empleo para oponerlo a derecha, lo empleo para definir esto que ustedes deben conocer bien: es que si quieren definir el enrulamiento de un caracol que como ustedes saben, es privilegiado -dextrógiro o levógiro, poco importa, esto depende de cómo ustedes definan uno u otro- este enrulamiento, ustedes encuentran el mismo miren el caracol del lado de su punta o lo den vuelta para mirarlo del lado del lugar donde él esboza una cavidad.
En otros términos, es que al dar vuelta aquí el cross-cap para verle del otro lado, si definimos aquí la rotación de la izquierda hacia la derecha alejándonos del punto central, ven que él gira siempre en el mismo sentido del otro lado.
Esta es la propiedad de todos los cuerpos que son disimétricos. Es entonces de una disimetría que se trata, fundamental en la forma de esta superficie.
La prueba es que ustedes tienen debato algo que es la imagen de esta superficie así definida sobre nuestro doble bucle, en el espejo. Hela ahí. Debemos esperar que, como en todo cuerpo disimétrico, la imagen en el espejo no le sea superponible, lo mismo que nuestra imagen en el espejo a nosotros que no somos simétricos a pesar de lo que creemos, no se superpone del todo a nuestro propio soporte. Si tenemos un lunar sobre la mejilla derecha, ese lunar estará sobre la mejilla izquierda de la imagen en el espejo.
No obstante, la propiedad de esta superficie es tal que como ven basta hacer subir un poquito este bucle -y es legítimo hacerlo pasar por encima del otro, ya que los dos planos no se atraviesan realmente para obtener una imagen (3) absolutamente idéntica y entonces superponible a la primera, a aquella de la que hemos partido (1)
Ven lo que ocurre: remonten esto suave y progresivamente hasta aquí y vean lo que va a ocurrir, a saber que la ocultación de esta partecita en puntillado situada aquí es la realización idéntica de lo que está en la imagen primitiva.
Esto nos sirve para ilustrar esta propiedad que les he dicho es la a en tanto que objeto de deseo, de ser algo que es a la vez orientatable y seguramente muy orientado, pero que no es, si me puedo expresar así especularizable.
En ese nivel radical que constituye el sujeto en su dependencia por relación al objeto del deseo, la función i de a, función especular, pierde su àpresamiento si se puede decir.
Y todo esto comandado, ¿porqué?
Por algo que es justamente ese punto (punto central) en tanto pertenece a esta superficie.
Para aclarar enseguida lo que quiero decir, les diré que es articulando la función de ese punto que podemos encontrar toda suerte de fórmulas felices que nos permiten concebir la función del falo en el centro de la constitución del objeto del deseo.
Es por esto que vale la pena que continuemos interesándonos en la estructura de ese punto.
Ese punto en tanto él es la clave de la estructura, de esta superficie así definida, recortada por nuestro corte en el plano proyectivo, ese punto, es necesario que me detenga un instante para mostrarles cual es su verdadera función. Es lo que les demandará seguramente todavía un poco de paciencia.
¿Cuál es la función de ese punto? Lo que ahí es manifiesto en ese momento en el que nos detenemos, es que está en una de las dos partes en las que está dividido por el doble corte el plano proyectivo. Pertenece a esta parte que se separa, no pertenece a la parte que queda (figura D).
En tanto parece han sido capaces hace un rato -debo al menos inferirlo del hecho de que no se ha elevado ningún murmullo de protesta- de concebir como esta figura puede pasar a aquélla por simple desplazamiento legitimo del nivel del corte, serán, pienso, también capaces de hacer el esfuerzo mental de ver lo que, sucede si por una parte, hacemos franquear el horizonte del callejón sin salida interior (fondo de la bolsa inferior) de la superficie en este corte haciéndola pasar entonces del otro lado, como lo indica mi flecha amarilla. y si hacemos franquear en la parte superior del bucle igualmente el horizonte de lo que está arriba del cross-cap.
Esto nos conduce sin dificultad a la figura siguiente.
El pasaje de la última es un poco más difícil de concebir, no por el bucle inferior como ven, sino por el bucle superior en la medida en que ustedes pueden quizás tener un instante de vacilación concerniente a lo que ocurre en el momento de franqueamiento de lo que aquí se presenta como la extremidad de la línea de penetración.
Si reflexionan un poco verán que si es del otro lado que el corte es llevado a franquear esta línea de penetración, evidentemente ella se presentara así, es decir como esta del otro lado estará en línea de puntos de este lados Y será plena ya que de acuerdo a nuestra convención lo que está en punteado es visto por transparencia.
Nada en la estructura de la superficie nos permite distinguir el valor de esos cortes 1 y 2, es decir aquellos a los cuales llegamos aquí. Para el ojo se presentan como entrando los dos del mismo lado de la línea de penetración.
¿Es muy simple para el ojo? Seguramente no. Pues esta diferencia que hay entre, por el corte de entrar desde dos lados diferentes o entrar por el mismo lado 3, es algo que debe asimismo señalarse en el resultado, sobre la figura. Y por otra parte, esto es absolutamente sensible. Si ustedes reflexionan en lo que es, lo que de aquí en más está recortado sobre esta superficie, lo reconocerán fácilmente: de entrada, es lo mismo que nuestro significante; además de la manera en que esto recorta una superficie, recorta una superficie que ustedes perciben bien -no tienen más que mirar la figura- que es una banda, una banda que no tiene más que un borde. Les he ya mostrado lo que es una banda de Moebius.
Ahora, las propiedades de una superficie de Moebius son propiedades completamente diferentes de aquellas de esta pequeña superficie giratoria de la que les he mostrado hace un rato las propiedades al darla vuelta, mirándola, transformándola y diciéndoles finalmente que es ésta la que nos interesa.
Esa pequeña vuelta de passe-passe tiene evidentemente una razón que no es difícil de encontrar. Su interés es simplemente mostrarles que este corte divide la superficie Siempre en dos partes, de las que una conserva el punto de que se trata en su interior, y de la que el otro no lo tiene más.
Esta otra parte que está tan presente en 1 como en la figura terminal 3, es una Superficie de Moebius. El doble corte divide siempre la superficie llamada cross-cap en dos: ese algo en lo que nos interesamos y de lo que voy a hacer para ustedes el soporte de la explicación de $ con a en el fantasma, y del otro lado una superficie de Moebius.
¿Cual es la primer cosa que les he hecho palpar cuando les obsequié estas cinco o seis superficies de Moebius que he lanzado a través de la asamblea?
Es que la superficie de Moebius, en el sentido en que la entiendo, es irreductiblemente izquierda. Cualquier modificación que le hagan sufrir, no podrán superponer su imagen en el espejo.
Ven la función de este corte y lo que él muestra de ejemplar, El es tal que dividiendo una cierta superficie de una manera privilegiada, superficie cuya naturaleza y función nos son completamente enigmáticas, puesto que ni bien la podemos situar en el espacio hace aparecer funciones privilegiadas de un lado, las que he llamado especularizable es decir de comportar su irreductibilidad a la imagen especular, y del otro lado, una, superficie que, aunque presentando todos los privilegios de una superficie orientada; no es especularizada, Pues, observen que esta superficie no se: puede decir, como sobre la superficie de Moebius, que un ser infinitamente plano, paseándose se encontrará de golpe sobre esta superficie en su propio revés: cada cara está separada de la otra en esto.
Esta propiedad seguramente es algo que deja abierto un enigma; pues no es tan simple, es por tanto menos simple que la superficie total -es bien evidente- no es reconstituible, y reconstituible inmediatamente sino a partir de esto:
Es necesario entonces que las propiedades más fundamentales de la superficie sea en alguna parte conservadas a pesar de su apariencia más racional que la del otro, en esta superficie.
Es absolutamente claro que están conservadas a nivel del punto. Si el pasaje que en la figura total vuelve siempre posible a un viajero infinitamente chato reencontrarse por un camino excesivamente breve en un punto que es su propio revés, digo: sobre la superficie total, -si no es más posible a nivel de la superficie central, fragmentada, dividida por el significante, del doble bucle, es que muy precisamente algo de esto está conservado a nivel del punto.
Con la salvedad de que justamente para que este punto funcione.. como ese punto, él tiene ese privilegio de ser justamente infranqueable, salvo haciendo desaparecer, si se puede decir, toda la estructura de la superficie.
Lo ven, no he incluso podido dar todavía su pleno desarrollo a lo que vengo de decir de ese punto. Si reflexionan podrán de aquí a la próxima vez encontrarlo ustedes mismos.
La hora es avanzada, y es aquí que estoy obligado a dejarlos. Me excuso de la aridez de lo que he sido llevado hoy a producir ante ustedes, por el hecho de la complejidad mismas aún cuando no sea sino una complejidad extraordinariamente puntiforme, es el caso de decirlo. Es desde aquí que retomaré la próxima vez.
Vuelvo entonces sobre lo que dije al comienzo el hecho de que no haya podido llegar sino hasta ese punto de mi exposición hará que mi seminario del miércoles próximo sea mantenido en el propósito de no dejar demasiado espacio, demasiado intervalo entre esos dos seminarios, pues ese espacio podría ser nocivo a la continuidad de nuestra explicación.